This blog post is the first in a series about machine learning algorithms for computer vision. In this post we will discuss how convolutional neural networks (CNNs) help computers understand images. The following posts will discuss how we can reuse CNNs in different domains without having to train new models – a process called transfer learning.
Computer vision is a broad category of algorithms that extract information from images. When you take a picture on your phone and see boxes around people’s faces, you are using computer vision. Many algorithms take advantage of real world heuristics to extract information from images. For example, a simple algorithm for detecting text in images can compare regions in an image to existing fonts until a match is found. This algorithm is quick to implement, but not robust enough for use in real world vision systems. For example, if the text is handwritten, this detector will fail to find any matches. In contrast, convolutional neural networks learn to extract robust features from images and work well in real world settings.

The iPhone camera detects faces using computer vision
Introduction to CNNs
Before we jump into designing CNNs, let’s start with the basics. Convolution is a math operation (like addition or multiplication) that combines a matrix, called the kernel, with an image to produce a new image. Convolutional neural networks apply stacks of convolutional kernels to extract features from images which are then fed into a classifier. The idea of using convolution kernels to extract features from data has been used in image processing for decades, from Photoshop filters to medical imaging. Below is a picture of a sobel kernel and the result of convolving the kernel with an image. Visually, we can see that the sobel kernel has enhanced the edges of our image. Pixels located near an edge are boosted, and everywhere else the pixel values are muted giving us an edge detector. By pulling out edge features from an image, the sobel kernel has made it easier to analyze images in terms of edges and non-edges. For example, we could measure the angles of the extracted edges and check if there are four edges that connect at 90 degree angles to give us a box detector.
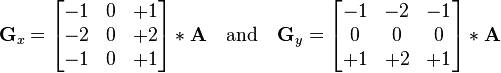
Sobel kernel matrices

From left: Original image, image after sobel kernel has been applied (Wikipedia)
The issue with hard coded kernels is that they only perform one task. Let’s say we wanted to write a program to apply the Nashville Instagram filter to our image. The Nashville filter is pretty complicated, and it’s somewhat tricky to guess which matrix we’ll need for our convolution kernel. Instead of guessing the kernel, we could take a random matrix as our kernel and repeatedly change its values until the resulting image looks like the Instagram filter. Doing this by hand would take a long time, so we’ll let our computers do the hard work for us. Suppose we had a dataset of pairs of filtered and unfiltered images. Our algorithm would start with a random kernel matrix, convolutionally apply the kernel to an unfiltered image, measure the error between the output and the filtered version of the image, then finally update the kernel to reduce that error. After enough iterations, our algorithm will discover the kernel that produces the desired effect.

From left: Original image, image after applying Nashville filter

Learned Instagram filters – from left: 1000 iterations, 3000 iterations, 999500 iterations
Whereas Instagram filters might not be useful for general purpose image recognition algorithms, this example demonstrates how to automate the learning process for any arbitrary output, using convolution kernels.
Instead of learning to replicate an Instagram filter, imagine how we could learn a convolution kernel that makes it easy to classify image. All we need is another piece to our algorithm, a classifier, which uses the result of the convolution to a make a guess about which category the image came from. We use the error between the classifier’s predicted category and the actual category to make a better convolutional filter for the next pass. Now, our algorithm will learn a kernel which will transform the image into something that the classifier portion of our algorithm can use to make predictions.
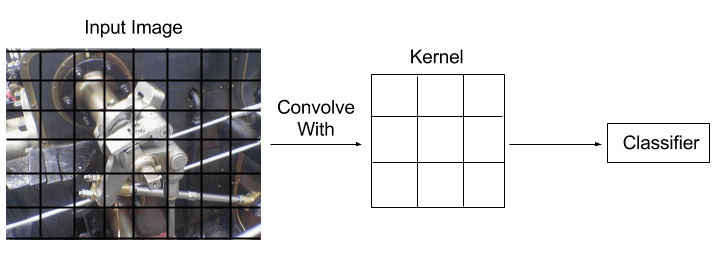
CNN classifier architecture
The algorithm described above would be considered a shallow CNN, since we only applied one layer of convolution before the classifier. Shallow CNNs are fine for some tasks, but are limited in what they can learn. To learn more sophisticated features, we feed the result of the first convolution layer to another convolution layer and send the result to a classifier. Now things are starting to get deep. With two convolution filters applied to our image, we can extract richer information that the classifier can use to make predictions. To go even deeper, we can add three, four, or however many convolution filters we want to our image–depth is limited by trainability and computational efficiency. We’ve now transitioned into deep convolutional networks.

Necessary Inception meme
The primary difference between deep and shallow CNNs is how many layers they contain. It’s not immediately obvious, but each successive application of convolution learns more complicated features. For example, the first convolution might learn to detect edges, the second might learn to compose those edges into corners, and the following layers might refine the rough shapes into complicated shapes, such as textures, that the classifier can use for predictions.
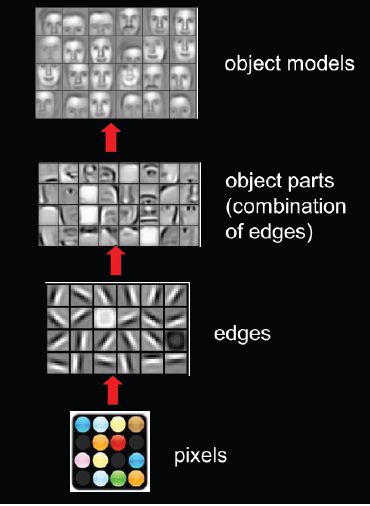
CNN layers extracting complex features
Another way to improve model accuracy is making it wider instead of deeper. To make a layer wider, we learn multiple convolution kernels from each layer. For example, let’s say we wanted a CNN to distinguish between different handwritten digits. If we only learned a single convolution kernel, we would need that kernel to somehow differentiate each of the different handwritten digits. If instead we had our model learn 100 different convolution filters, each kernel would only be responsible for extracting a small feature which can be used to identify numbers. For example, one filter might learn to look for large loops, indicating that the number is probably a 0 or 8. Another filter might learn to look for lines which go through the middle of a number, distinguishing between 0 and 8. In contrast, single filter architectures would need their kernel to learn how to encode both of those filters and how to distinguish between the other numbers. Therefore, adding wider layers to our CNN simplifies the task for each convolution kernel, improving the model’s ability to learn.

Visualization of kernels in a single layer from a CNN trained to recognize handwritten digits
The magic of convolutional neural networks is that they learn how to convert images into useful features that a classifier can use for prediction. There are no hand-defined rules here. CNNs provide us with a generalized algorithm that works on a wide variety of images without requiring any domain knowledge of what it is trying to classify.
We’ve concluded Part I of our computer vision blog post series. In the next post, we will discuss how CNNs trained on one class of images can still make accurate predictions on entirely different classes of images. If you have any questions or need help getting started, feel free to reach out to us at contact@indico.io!



